What is the meaning of PVT corners & How these corners will affect the Delay?
How OCV (On-Chip Variation)is related to PVT?
PVT:
PVT is the Process, Voltage, and Temperature. In order to make our chip to work after fabrication in all the possible conditions, we simulate it at different corners of process, voltage, and temperature. These conditions are called corners. All these three parameters directly affect the delay of the cell.
Process:
There are millions of transistors on the single-chip as we are going to lower nodes and all the transistors in a chip cannot have the same properties. Process variation is the deviation in parameters of the transistor during the fabrication.
During manufacturing a die, the area at the center and at the boundary will have different process variations. This happens because layers that will be getting fabricated cannot be uniform all over the die.
Below are a few important factors which can cause the process
variation;
- The wavelength of the UV light
- Manufacturing defects
- Oxide thickness variation
- Dopant and mobility fluctuation
- Transistor width
- RC Variation
- channel length
- doping concentration,
- metal thickness
- impurity concentration densities
- diffusion depths
- imperfections in the manufacturing process like mask print, etching
These variations will cause the parameters like threshold voltage
and threshold voltage depends on different parameters like doping
concentration, surface potential, channel length, oxide thickness, temperature,
source-to-body voltage, and implant impurities, etc.
The threshold voltage equals the sum of the flat band voltage,
twice the bulk potential, and the voltage across the oxide due to the depletion
layer charge.
So, the current flowing through the channel
directly depends upon
- Mobility (μn), (mobility is depending upon temperature)
- Oxide capacitance Cox (and Cox = εox/ tox hence the thickness of oxide i.e. tox)
- The ratio of width to length (W/L)
If any of these parameters change, it will change the current and change in current will affect the delay of the circuit because The delay depends upon the R and C values (Time constant RC) of the circuit. The relation between process and delay shown in Figure. From the figure, we conclude that delay is more for slow process MOSFETs and it is less for fast process MOSFETs.
The process of fabrication includes Oxidation,
diffusion, Ion Implantation, Deposition, Etching, Photolithography, drawing out
of metal wires, gate drawing, etc. The diffusion density and the width of metal
wire are not uniform throughout wafer and diffusion regions for all transistors
will not have the same diffusion concentrations. So, all transistors are
expected to have different characteristics. This introduces variations in the
sheet resistance (Rs) and transistor parameters such as threshold voltage (Vth)
and because of this, it will causes (W/L) variations in MOS transistors.
Process variation is different for different
technologies but is more dominant in lower node technologies because transistors
are in millions on the chip. Process variations are due to variations in the
manufacturing conditions such as temperature, pressure, and dopant
concentrations. As a consequence, the
different transistors have different lengths throughout the chip. This makes
the different propagation delay everywhere in a chip because a smaller
transistor is faster and therefore the propagation delay is smaller.
Voltage:
As we are going to the
lower nodes the supply voltage for a chip is also going to less. Let’s say the
chip is operating at 1.2V. So, there are chances that at certain instances of
time this voltage may vary. It can go to 1.5V or 0.8V. To take care of this scenario,
we consider voltage variation.
There are multiple
reasons for voltage variation.
- IR drop is caused by the current flow over the power grid network.
- Supply noise caused by parasitic inductance in combination with resistance and capacitance. when the current is flowing through parasitic inductance (L) it will causes the voltage bounce.
The supply voltage is
given to any chip either externally from the DC source or some voltage
regulator. The voltage regulator will not give the same voltage all the time.
It can go above or below to the expected voltage and hence if voltage change it
will change the current and making the circuit slower or faster than earlier.
Power is distributed to all transistors on the chip with the help of a power grid network. Throughout a chip, the power supply is not constant it will change with the placement of cells. The power grid network is made up of metals and metals have their own resistance and capacitance. So, there is a voltage drop along the power grid.
The supply voltage reaching the power pins will not be the same for all standard cells and macros because of the resistance variation of the metals. Consider there are two cells, one which is placed closer to the DC power source, and others placed far. As the interconnect length is more for the farther cell, it has more resistance and results in a higher IR drop, and it reduces the supply voltage reaching the farthest cell. As the voltage is less, this cell will take more delay to power on than the cell which is placed closer. If nearer cells get higher voltage then the cell is faster and hence the propagation delay is also reduced. That is the reason because of which, there is variation in delays across the transistors.
The delay of a cell is depending on the saturation current and the saturation current of a cell depends on the power supply. In this way, the power supply affects the propagation delay of a cell.
The self-inductance of a supply line contributes also to a voltage drop. For example, when a transistor is switching to high, it takes a current to charge up the output load. This time-varying current (for a short period of time) causes an opposite self-induced electromotive force. The amplitude of the voltage drop is given by V=L*dI/dt, where L is the self-inductance and I is the current through the line.
Temperature:
The transistor density is not uniform throughout
the chip. Some regions of the chip have higher density and higher switching,
resulting in higher power dissipation and Some regions of the chip have lower
density and lower switching, resulting in lower power dissipation Hence the
junction temperature at these regions may be higher or lower depending upon the
density of transistors. Because of the variation in temperature across the
chip, it introduces different delays across all the transistors.
The temperature variation is with respect to the
junction and not ambient temperature. The temperature at the junction inside
the chip can vary within a big range and that’s why temperature variation needs
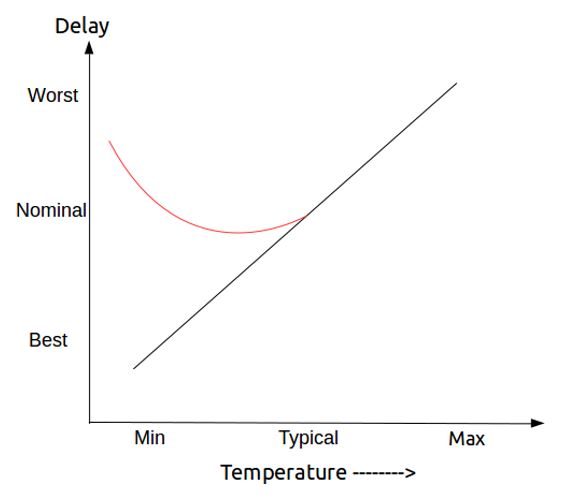
to be considered. Delay of a cell increases with an increase in temperature.
But this is not true for all technology nodes. For deep sub-micron
technologies, this behavior is contrary. This phenomenon is called a
temperature inversion.
When a chip is operating, the temperature can vary throughout the chip. This is due to the power dissipation in the MOS-transistors. The power consumption in the transistors is mainly due to switching, short-circuit, and leakage power consumption.
The average switching power dissipation is due to the required energy to charge up the parasitic and load capacitances and the short-circuit power dissipation is due to the finite rise and fall times and leakage power consumption is due to the reverse leakage and sub-threshold currents.
The biggest contribution to power consumption is
switching. The dissipated power will increase the temperature. Mobility depends
on temperature.
mobility= temp^-m
we know that with an increase in temperature, the resistivity of a metal wire(conductor) increases. The reason for this phenomenon is that with an increase in temperature, thermal vibrations also increase. This gives rise to increased electron scattering and electrons start colliding with each other more and the mobility of the primary carriers decreases with an increase in temperature.
Similarly, for higher doping concentrations, the temperature is higher and thermal vibrations are also increasing and the electrons and holes move slower i.e. mobility decreases, then the propagation delay increases. Hence, the propagation delay increases with increased temperature. The threshold voltage of a transistor depends on the temperature. A higher temperature will decrease the threshold voltage. A lower threshold voltage means a higher current and therefore a better delay performance. This effect depends extremely on the power supply, threshold voltage, load, and input slope of a cell. There is a competition between the two effects and generally the mobility effect wins.


I found so many interesting stuff in your blog especially its discussion. From the tons of comments on your articles, I guess I am not the only one having all the enjoyment here! keep up the good work... ux-fob
ReplyDeleteChanging a Voltmeter to Multiple Sources in Series
ReplyDeleteWhile changing a voltmeter to a series line of 30 voltage sources (VS),عالية الجهد مكثف السيراميك